ROZDZIAŁ 9. SUPLEMENT 2
SYMETRIA PASM W PIERWSZEJ STREFIE BRILLOUINA
Plik pdf do wydruku:
r9_supl2.pdf
Równanie orbitalne dla kryształu ma postać
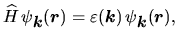 |
(1) |
gdzie jednoelektronowy efektywny hamiltonian
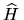
można (w j.at.)
zapisać jako:
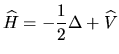 |
(2) |
z potencjałem
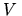
o symetrii kryształu. Funkcja falowa musi należeć,
jak zawsze, do jednej z nieprzywiedlnych reprezentacji grupy symetrii kryształu i dlatego możemy jej dać indeks
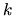
, oznaczający wektor falowy determinujący reprezentację nieprzywiedlną grupy translacji. Jeśli tak, to i wartość własna
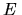
zależy od przyjętego
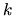
, stąd
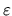
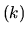
.
Nie znamy postaci
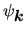
, ale wiemy, że
funkcja ta musi zachowywać się
tak, jak wynika z twierdzenia Blocha. Jest to zagwarantowane bez straty ogólności, jeśli
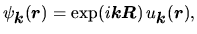 |
(3) |
gdzie
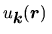
ma taką samą symetrię
jak kryształ lub jak
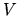
. W tej sytuacji zamiast
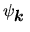
wystarczy poszukać
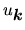
.
Zainteresujemy się, jakie równanie powinno spełniać
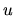
?
Wstawiamy równanie (3) do równania orbitalnego i dostajemy
Potrzebne nam będzie działanie operatora

na duży nawias:
Równanie na
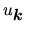
przybiera postać
czyli
Jest to równanie własne na
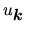
i
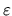
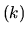
.
Równanie to może mieć wiele rozwiązań, które będziemy numerować indeksem
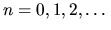
Stąd otrzymamy
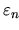
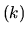
,
a to oznacza
strukturę pasmową
-- energia zależy od wektora
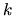
zgodnie z tym, że komórki elementarne oddziałują wiążąco i antywiążąco na różne sposoby, ale dzieje się to w ramach jednego pasma o określonym

. Mogą być też inne rozwiązania na
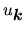
, które
w naszych dotychczasowych przykładach odpowiadałyby innym (np. wzbudzonym)
orbitalom w węzłach sieci i powstałyby inne pasma o innych

.
W zasadzie nie byłoby potrzeby wypisywania tego równania na
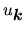 ,
gdyby nie to, że chcę za jego pomocą wykazać, że struktura pasmowa
,
gdyby nie to, że chcę za jego pomocą wykazać, że struktura pasmowa
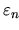
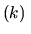 w PSB
(pierwszej strefie Brillouina) ma taką samą symetrię jak sam kryształ.
w PSB
(pierwszej strefie Brillouina) ma taką samą symetrię jak sam kryształ.
Teraz to udowodnimy.
Każda operacja symetrii
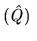 kryształu spełnia równanie
kryształu spełnia równanie
Odpowiada temu pewna liniowa transformacja współrzędnych; nowe współrzędne jakiegoś punktu wyrażają się jako liniowe kombinacje starych współrzędnych tego punktu
1:
przy czym
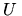
jest macierzą ortogonalną, tzn.
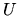
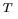
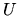
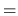
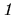
,
bo żadne odległości w obiekcie nie mają
prawa ulec zmianie, a to właśnie zapewnia transformacja ortogonalna.
Dokonajmy takiego samego przekształcenia wektora
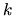
:
Napiszmy równanie na
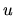
w nowym układzie współrzędnych:
Transformacja ortogonalna nie zmienia długości wektora
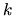
,
stąd
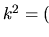
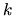
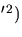
. Dalej,
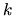
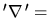
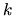
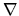
,
bo iloczyn skalarny zależy od wzajemnego położenia dwóch wektorów, a nie od tego, jak cały układ np. obrócono. W ten sposób jesteśmy przygotowani do przekształcenia drugiego i trzeciego członu. Jeśli chodzi o człon pierwszy, to również
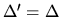
, co pokazano w rozdz. 2 podręcznika.
W rezultacie nasze równanie można zapisać w postaci
Jest to równanie własne z tym samym operatorem, co równanie przed transformacją, wobec tego
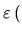
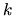
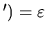
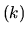
.
To właśnie mieliśmy wykazać:
- ... punktu1
-
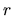
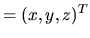 i
i
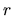
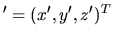 ;
podobnie
;
podobnie
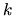

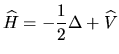
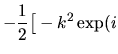
![]() ,
gdyby nie to, że chcę za jego pomocą wykazać, że struktura pasmowa
,
gdyby nie to, że chcę za jego pomocą wykazać, że struktura pasmowa
![]()
![]() w PSB
(pierwszej strefie Brillouina) ma taką samą symetrię jak sam kryształ.
w PSB
(pierwszej strefie Brillouina) ma taką samą symetrię jak sam kryształ.
![]() kryształu spełnia równanie
kryształu spełnia równanie
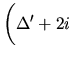
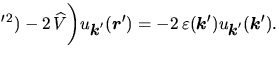

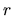
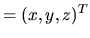 i
i
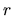
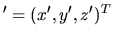 ;
podobnie
;
podobnie