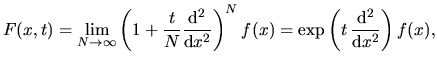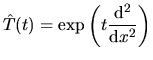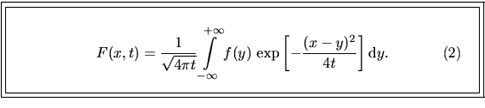ROZDZIAŁ 7. SUPLEMENT 1
METODA DYFUZYJNA
Plik pdf do wydruku: r7_supl1.pdf
Opisana metoda1 jest ogólna, można ją stosować w każdej dziedzinie, w której pojawiają się problemy minimalizacji funkcji o wielu minimach. Jest to metoda przybliżona, nie dająca gwarancji, że znalezione minimum jest minimum globalnym2. w taki sposób, aby najpierw (przy mniejszym parametrze deformacji) zaczęły znikać płytkie studnie potencjału, podczas gdy inne studnie rosłyby ich kosztem. Przy dalszej deformacji (większy parametr deformacji) zaczęłyby znikać głębsze minima. W tej metodzie zakłada się, że jedyna studnia, która pozostaje przy dużej deformacji, pochodzi od najgłębszego minimum (czyli globalnego) oryginalnej hiperpowierzchni energii potencjalnej.
Podczas takiej deformacji studnie potencjału zmniejszają
stopniowo swoją głębokość, zmieniają swój kształt i położenie. To powoduje, że położenie jedynego minimum, uzyskanego przy dużej deformacji, nie odpowiada dokładnie pozycji minimum globalnego (jeśli nasze założenie o tym, że przeżyje minimum globalne, jest słuszne).
Procedura powrotu
Pozycję minimum globalnego pierwotnej funkcji staramy się
odtworzyć, postępując w następujący sposób. Minimalizując energię
przy dostatecznie dużej wartości parametru deformacji, otrzymujemy położenie jedynego minimum. To położenie stanowi dla nas punkt startowy w procedurze powrotu. Procedura powrotu polega na tym, że zmniejszamy o pewną małą wartość parametr deformacji i minimalizujemy energię przy nowej wartości parametru, startując jednak z położenia w przestrzeni położeń jąder określonego przy użyciu
starej (większej) wartości tego parametru. Uzyskujemy nową
konfigurację jąder. Powtarzając ten krok wielokrotnie, wykreślamy trajektorię w przestrzeni położeń jąder jako funkcję zmniejszanego parametru deformacji. Na końcu parametr deformacji jest równy zeru i otrzymujemy położenie końcowe wspomnianej trajektorii. Jest to punkt startowy minimalizacji wyjściowej (niezdeformowanej) funkcji, w której osiągamy dno lokalnego basenu ![]() . Mamy nadzieję, że uzyskane minimum jest minimum globalnym. W jakim stopniu założenie to jest słuszne,
pokażą przykłady numeryczne.
. Mamy nadzieję, że uzyskane minimum jest minimum globalnym. W jakim stopniu założenie to jest słuszne,
pokażą przykłady numeryczne.
Jak deformować funkcję
Po tym opisie głównej idei metody przystąpmy do jej praktycznego sformułowania. Łatwo wygładzić koc, zasadniczą rzeczą jest pokazanie, w jaki sposób wygładzić pierwotną funkcję3.
Sformułowanie teorii podamy wpierw dla funkcji jednej zmiennej, a potem uogólnimy otrzymane rezultaty na przypadek wielu zmiennych. Weźmy funkcję
![]() i wykonajmy na niej prostą operację:
i wykonajmy na niej prostą operację:
Zwróćmy uwagę, że transformacja
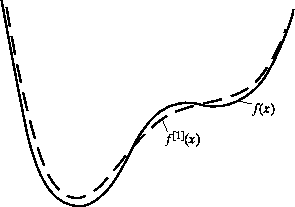
|
Rys.1. Destabilizacja basenów funkcji przez dodanie jej drugiej pochodnej. Krzywa przerywana |
Destabilizacja jest tym pewniejsza4, im mniejsze jest
![]() . Jest to spełnione, gdy
. Jest to spełnione, gdy
![]() , gdzie
, gdzie ![]() jest pewnym parametrem, zwanym parametrem deformacji, a
jest pewnym parametrem, zwanym parametrem deformacji, a ![]() jest bardzo duże.
Gdy
jest bardzo duże.
Gdy ![]() dąży do nieskończoności i procedura jest zbieżna, otrzymuje się w granicy funkcję
dąży do nieskończoności i procedura jest zbieżna, otrzymuje się w granicy funkcję ![]() :
:
przy czym
Operator
ma kilka interesujących właściwości. Po pierwsze, jego funkcjami własnymi są funkcje
Najciekawsza jest wartość własna
Istotnie,
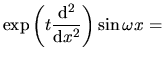 |
||
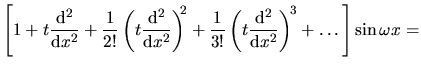 |
||
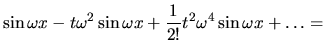 |
||
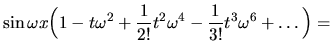 |
||
Podobny wynik uzyskalibyśmy dla
Ze wzorów (4) i (5) wynika, że operator
![]() dla
dla ![]() powoduje zmniejszenie amplitudy funkcji sinus i cosinus. Ważne jest to, że to spłaszczenie jest tym większe, im wyższej częstości
powoduje zmniejszenie amplitudy funkcji sinus i cosinus. Ważne jest to, że to spłaszczenie jest tym większe, im wyższej częstości ![]() odpowiada funkcja i im większy jest parametr deformacji
odpowiada funkcja i im większy jest parametr deformacji ![]() . Konsekwencją tego faktu jest to, że jeśli operator
. Konsekwencją tego faktu jest to, że jeśli operator
![]() zadziała na funkcję
zadziała na funkcję ![]() przedstawioną w postaci szeregu Fouriera, to przy wzroście parametru
przedstawioną w postaci szeregu Fouriera, to przy wzroście parametru ![]() najszybciej będą znikać składowe o wysokiej częstości.
najszybciej będą znikać składowe o wysokiej częstości.
![]() jest więc ,,mordercą wysokich częstości''.
jest więc ,,mordercą wysokich częstości''.
Równanie dyfuzji
Bardzo łatwo przekonać się, że jeśli szereg Taylora w równ. (2) jest zbieżny, to:
w którym parametr Alternatywne postacie transformacji
Jest kilka alternatywnych postaci funkcji7 ![]() . Wyraża się ona
. Wyraża się ona
- albo jako rezultat działania operatora
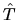 na funkcję
na funkcję 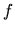 ,
,
- albo jako rozwiązanie równania dyfuzji,
- albo w bardzo przydatnej postaci jako splot
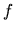 z funkcją gaussowską:
z funkcją gaussowską:
Jeśli wpatrzeć się w funkcję podcałkową, to można zauważyć, że wygładzanie funkcji ![]() (rezultat to
(rezultat to ![]() ) polega na lokalnym uśrednianiu jej wartości w każdym punkcie
) polega na lokalnym uśrednianiu jej wartości w każdym punkcie ![]() z wagą gaussowską, przy czym im większe
z wagą gaussowską, przy czym im większe
![]() , tym szerszy zasięg uśredniania. Gdy
, tym szerszy zasięg uśredniania. Gdy ![]() , funkcja gaussowska przechodzi w funkcję
, funkcja gaussowska przechodzi w funkcję ![]() Diraca, co oznacza brak uśredniania,
Diraca, co oznacza brak uśredniania,
![]() .
.
Funkcja ![]() przyjęła, dzięki interpretacji poprzez równanie dyfuzji, znaczenie temperatury (gdy rozpatrujemy przepływ ciepła)
lub znaczenie stężenia (gdy rozpatrujemy transport substancji w ośrodku).
Ta interpretacja fizyczna sugeruje od razu, że w pewnych przypadkach minimum globalnego tą metodą znaleźć się nie da. Na przykład jeśli minimum globalne odpowiada wąskiej studni, to może się zdarzyć, że przy
wzroście czasu ta właśnie studnia potencjału znika, podczas gdy inna, może nie tak głęboka, ale dostatecznie szeroka, pozostaje. Można jednak zadać pytanie, czy chemika powinny interesować wąskie studnie potencjału (nawet jeśli są głębokie). Istotnie, szerokie studnie (dużo stanów oscylacyjnych) są faworyzowane entropowo, co powoduje obniżenie energii swobodnej.
przyjęła, dzięki interpretacji poprzez równanie dyfuzji, znaczenie temperatury (gdy rozpatrujemy przepływ ciepła)
lub znaczenie stężenia (gdy rozpatrujemy transport substancji w ośrodku).
Ta interpretacja fizyczna sugeruje od razu, że w pewnych przypadkach minimum globalnego tą metodą znaleźć się nie da. Na przykład jeśli minimum globalne odpowiada wąskiej studni, to może się zdarzyć, że przy
wzroście czasu ta właśnie studnia potencjału znika, podczas gdy inna, może nie tak głęboka, ale dostatecznie szeroka, pozostaje. Można jednak zadać pytanie, czy chemika powinny interesować wąskie studnie potencjału (nawet jeśli są głębokie). Istotnie, szerokie studnie (dużo stanów oscylacyjnych) są faworyzowane entropowo, co powoduje obniżenie energii swobodnej.
Ograniczymy się do zastosowania przedstawionej metody do dwóch przykładów nie związanych z chemią.
Przykład 1.
Funkcja
![]() ,
, ![]() ,
, ![]() ma dwa minima: lokalne dla
ma dwa minima: lokalne dla
![]() i globalne dla
i globalne dla
![]() oraz jedno maksimum dla
oraz jedno maksimum dla ![]() .
Zastosowanie operatora
.
Zastosowanie operatora
![]() do funkcji
do funkcji ![]() daje:
daje:
co oznacza, że ze wzrostem
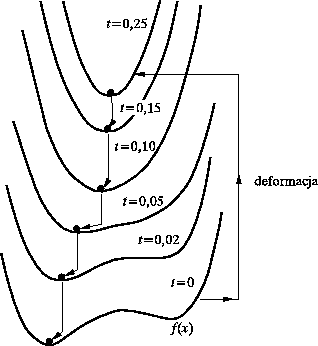
|
Rys 2. Deformacja oryginalnego potencjału |
Przykład 2.
W literaturze dotyczącej globalnej minimalizacji poszukiwano minimum globalnego tzw. funkcji Bohachevskiego (rys.3):
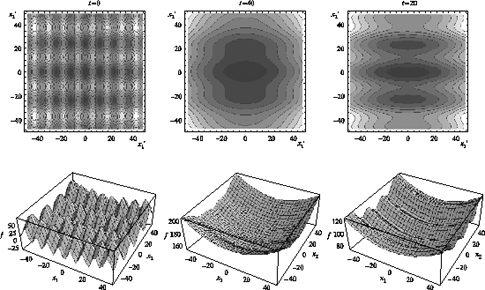 |
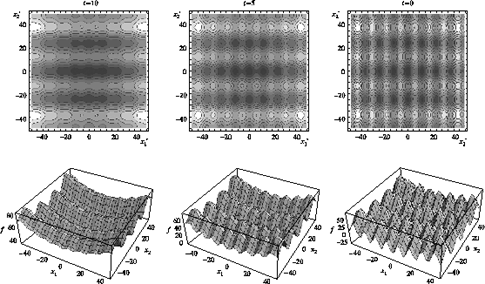 |
| Rys.3. Deformacja funkcji Bohachevskiego
|
Metoda dyfuzyjna osiąga rozwiązanie w następujący sposób. Po zadziałaniu na funkcję ![]() operatorem
operatorem
![]() otrzymujemy funkcję
otrzymujemy funkcję
![]() :
:
Gdy
Te i podobne przykłady dla funkcji w wielu wymiarach, a także przykłady z klasterami atomowymi wskazują, że w wielu przypadkach metodą dyfuzyjną
znajduje się minimum globalne. Czasem zamiast minimum globalnego metoda wskazuje szeroką studnię potencjału o niskiej, choć nie najniższej energii.
Reguły ewolucji
Idea metody dyfuzyjnej9została później związana z równaniami ewolucji pewnych wielkości fizycznych -- równaniem Schrödingera ewolucji funkcji falowej w czasie10, równaniem Blocha ewolucji rozkładu kanonicznego przy zmianie temperatury11, równaniami Smoluchowskiego i Fokkera-Plancka ewolucji pewnego rozkładu cząstek w czasie12 i zasadą wariacyjną Gibbsa dla energii swobodnej13.

Zwracało uwagę to, że mimo rozpatrywania szerokiej gamy zjawisk otrzymywane równania na trajektorię pozycji i szerokości funkcji gaussowskiej były podobne do siebie! Te obserwacje doprowadziły do uogólnienia, wyjaśniającego w pewnym stopniu, dlaczego przyroda nie ma wielkich problemów z globalną optymalizacją14. Oto w skrócie ta idea zastosowana do ewolucji położenia i szerokości funkcji gaussowskiej.
Załóżmy, że postęp optymalizacji kontroluje parametr ![]() , który zmienia się od 0 do wartości maksymalnej
, który zmienia się od 0 do wartości maksymalnej
![]() w sposób
,,ziarnisty'', tzn. tyka ,,zegar optymalizacji''. Za każdym tyknięciem
w sposób
,,ziarnisty'', tzn. tyka ,,zegar optymalizacji''. Za każdym tyknięciem
![]() zwiększa się o
zwiększa się o
![]() , gdzie
, gdzie ![]() jest liczbą kroków optymalizacji, i zmienia się pozycja
jest liczbą kroków optymalizacji, i zmienia się pozycja ![]() oraz
,,szerokość'' mierzona parametrem
oraz
,,szerokość'' mierzona parametrem ![]() funkcji gaussowskiej. O ile się
zmieniają te dwie wielkości? Okazuje się, że w różnych wspomnianych procedurach różnie, ale według bardzo podobnych równań różniczkowych:
funkcji gaussowskiej. O ile się
zmieniają te dwie wielkości? Okazuje się, że w różnych wspomnianych procedurach różnie, ale według bardzo podobnych równań różniczkowych:
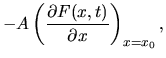 |
(10) | ||
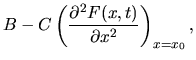 |
(11) |
w których
W skrócie można powiedzieć, że strategia stojąca za wspomnianymi równaniami ewolucji jest następująca:
- Należy używać nie potencjału
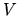 , lecz
, lecz 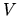 uśrednionego przez splot
uśrednionego przez splot 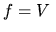 z funkcją gaussowską według
wzoru (8), czyli
z funkcją gaussowską według
wzoru (8), czyli 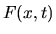 . Oba równania mówią, że parametr uśrednienia, czyli ,,czas''
. Oba równania mówią, że parametr uśrednienia, czyli ,,czas'' 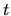 , jest funkcją położenia
, jest funkcją położenia 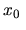 funkcji gaussowskiej.
funkcji gaussowskiej.
- Jak wynika z równ. (12), po starcie z jakiegoś położenia
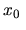 trzeba zawsze iść w dół uśrednionego potencjału
trzeba zawsze iść w dół uśrednionego potencjału
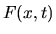 , czyli kierunek marszu to
, czyli kierunek marszu to
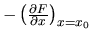 .
.
- Jak wynika z równ. (13), uśrednienie przez splot z funkcją
gaussowską o szerokości
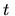 staje się mniej istotne dla
staje się mniej istotne dla 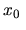 w pobliżu minimów [dodatnia wartość krzywizny krzywej, czyli drugiej pochodnej we wzorze (13) powoduje zmniejszenie
w pobliżu minimów [dodatnia wartość krzywizny krzywej, czyli drugiej pochodnej we wzorze (13) powoduje zmniejszenie 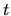 ] i bardzo istotne dla
] i bardzo istotne dla
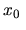 w pobliżu maksimów (ujemna wartość tej drugiej pochodnej powoduje zwiększenie
w pobliżu maksimów (ujemna wartość tej drugiej pochodnej powoduje zwiększenie 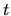 ). Dzięki ostatniej właściwości to maksimum może zacząć znikać, a wtedy przekroczymy barierę dzielącą dwa minima i możemy dotrzeć do minimum niższego!
). Dzięki ostatniej właściwości to maksimum może zacząć znikać, a wtedy przekroczymy barierę dzielącą dwa minima i możemy dotrzeć do minimum niższego!
- Z równania (13) wynika, że jeśli znajdujemy się na płaskowyżu lub w basenie o małej krzywiźnie krzywej, to zakres uśrednienia
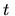 zaczyna się zwiększać15. Oznacza to, że, podczas zwiększania
zaczyna się zwiększać15. Oznacza to, że, podczas zwiększania 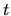 , uśrednienie może objąć pozycję jakiegoś dalekiego minimum, a wtedy
, uśrednienie może objąć pozycję jakiegoś dalekiego minimum, a wtedy
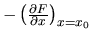 może nas do tego minimum zaprowadzić przez równ. (12).
może nas do tego minimum zaprowadzić przez równ. (12).
Wydaje się, że ten algorytm nie robi tylko jednej rzeczy, którą robi przyroda: nie potrafi podzielić jednego zwartego rozkładu na kilka takich rozkładów. Ta modyfikacja została wprowadzona w metodzie dyfuzyjnej przez Davida Shallowaya16.
- ... metoda1
-
Na tę ideę wpadłem, gdy leżałem chory na grypę w łóżku i przemyśliwałem,
jakby tu dobrać się do minimum globalnego. Koc przede mną miał liczne minima lokalne i jedno globalne. Gdy zacząłem naciągać koc, najpierw zaczęły znikać małe dolinki, a w końcu zostało jedno minimum --
ostatni ślad minimum globalnego. Wtedy bardzo łatwo mogłem tam trafić,
zjeżdżając z dowolnego punktu koca.
W książce ,,The Character of Physical Law'' (Cox and Wyman Ltd, London 1965) Richard Feynman napisał słowa, które bardzo pasują do mojej przygody z deformacją funkcji: ,,Moja idea wydawała mi się tak logiczna i tak elegancka, że zakochałem się w niej bez pamięci. A przecież zakochać się bez pamięci w dziewczynie można tylko wtedy, gdy jeszcze jej dobrze nie znasz i nie widzisz wszystkich jej wad. Wady zobaczysz później, ale miłość jest już dostatecznie silna, żeby cię zatrzymać'' (tłum. L. P.).
- ... globalnym2
- Nie jest to szczególna cecha tej metody -- taka metoda nie istnieje.
- ... funkcję3
- Tego jeszcze podczas grypy nie wiedziałem. W roku 1987 byłem na Uniwersytecie w Namur w Belgii i kupiłem dla syna komputer, którym wieczorem się bawiłem. Podczas zabawy z wykresami funkcji zobaczyłem to, co jest opisane poniżej we wzorach (1) i (2).
- ... pewniejsza4
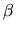 nie może być zbyt duże. W skrajnym przypadku prowadziłoby to do zastąpienia funkcji
nie może być zbyt duże. W skrajnym przypadku prowadziłoby to do zastąpienia funkcji 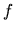 funkcją
funkcją
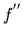 , a to jest niecelowe, bo ta ostatnia nie jest wygładzoną funkcją
, a to jest niecelowe, bo ta ostatnia nie jest wygładzoną funkcją 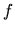 .
.
- ...czasu5
- Jest to nieoczekiwane. Problem jest czysto matematyczny i nagle pojawia się w nim czas!
- ... jest6
- Równanie (7) sprawdzimy w następujący sposób:
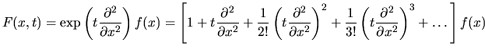
Prawa strona równ. (7):
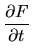
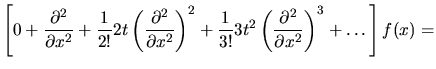
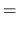
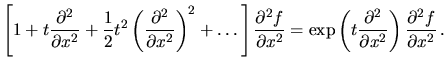
Lewa strona równ. (7):
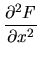
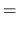
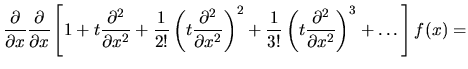
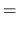
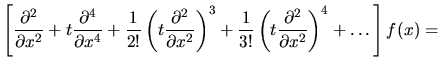
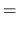
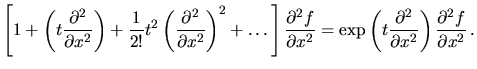
A więc lewa strona równ. (7) równa się stronie prawej, c.b.d.o. - ... funkcji7
- Postaci te różnią się domenami funkcji, do których procedury wygładzania mogą być aplikowane.
- ... inni8
- I. O. Bohachevsky, M. E. Johnson, M. L. Stein, Technometrics,
 . Trzeba przyznać, że funkcja Bohachevskiego jest szczególnie
łatwym łupem metody dyfuzyjnej. Jest tak jeszcze w przypadku kilku podobnych funkcji. Metoda natrafia jednak na poważne trudności przy zagadnieniach
o praktycznym znaczeniu w chemii (np. dużych molekułach wieloatomowych).
. Trzeba przyznać, że funkcja Bohachevskiego jest szczególnie
łatwym łupem metody dyfuzyjnej. Jest tak jeszcze w przypadku kilku podobnych funkcji. Metoda natrafia jednak na poważne trudności przy zagadnieniach
o praktycznym znaczeniu w chemii (np. dużych molekułach wieloatomowych).
- ... dyfuzyjnej9
-
L. Piela, J. Kostrowicki, H. Scheraga,
J. Phys. Chem.,
 .
.
- ...czasie10
-
P. Amara, D. Hsu, J. E. Straub, J. Phys. Chem.,
 .
.
- ...temperatury11
-
J. Ma, J. E. Straub, J. Chem. Phys.,
 .
.
- ...czasie12
-
J. E. Straub, J. Ma, P. Amara, J. Chem. Phys.,
 .
.
- ... swobodnej13
-
S. Schelstraete i H. Verschelde, J. Chem. Phys.,
 ,
wykorzystali do globalnej optymalizacji zasadę wariacyjną Gibbsa mówiącą, że entalpia swobodna (energia swobodna Gibbsa) to minimum pewnego funkcjonału w zbiorze znormalizowanych rozkładów gęstości
,
wykorzystali do globalnej optymalizacji zasadę wariacyjną Gibbsa mówiącą, że entalpia swobodna (energia swobodna Gibbsa) to minimum pewnego funkcjonału w zbiorze znormalizowanych rozkładów gęstości 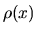 , który autorzy aproksymowali funkcją gaussowską o zmiennej pozycji i szerokości. Startując z szerokiej funkcji gaussowskiej o dowolnym położeniu, dostaje się (podczas minimalizacji funkcjonału energii swobodnej) trajektorię jej położeń i trajektorię jej szerokości.
Obie trajektorie zawierają funkcję
, który autorzy aproksymowali funkcją gaussowską o zmiennej pozycji i szerokości. Startując z szerokiej funkcji gaussowskiej o dowolnym położeniu, dostaje się (podczas minimalizacji funkcjonału energii swobodnej) trajektorię jej położeń i trajektorię jej szerokości.
Obie trajektorie zawierają funkcję 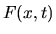 , z potencjałem
, z potencjałem 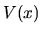 jako odpowiednikiem
jako odpowiednikiem 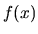 . Oprócz jednak wyrażenia na
. Oprócz jednak wyrażenia na 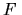 występuje tam człon entropowy. Związanie metody dyfuzyjnej z entropią i entalpią
swobodną jest wielkim osiągnięciem autorów.
występuje tam człon entropowy. Związanie metody dyfuzyjnej z entropią i entalpią
swobodną jest wielkim osiągnięciem autorów.
- ... optymalizacją14
-
L. Piela, Collect. Czech. Chem. Commun.,
 .
.
- ... zwiększać15
- Jest to ,,polowanie'' na dalekie minima.
- ... Shallowaya16
- D. Shalloway, w ,,Recent Advances in Global Optimization'', red. A. Floudas i P. M. Pardalos, Princeton University, Princeton 1992.