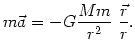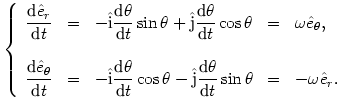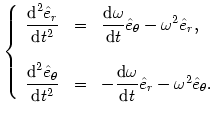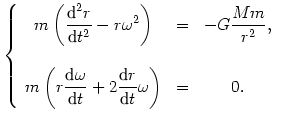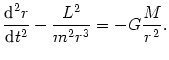Wyprowadzenie praw Keplera (derivation of Kepler's laws)

Trzy prawa Keplera dotyczą ruchów planet wokół Słońca i mają postać:

Pierwsze prawo Keplera.

Wszystkie planety poruszają się po orbitach w kształcie elipsy, w której jednym z ognisk znajduje się Słońce.

Drugie prawo Keplera.

Linia łącząca planetę ze Słońcem zakreśla w jednakowych odstępach czasu jednakowe pola powierzchni w płaszczyźnie orbity. Oznacza to, że wielkość jest stała, przy czym oznacza pole powierzchni zakreślone przez tę linię.

Trzecie prawo Keplera

Kwadrat okresu ruchu każdej planety na orbicie wokół Słońca jest proporcjonalny do sześcianu półosi wielkiej tej orbity.

Dowód:

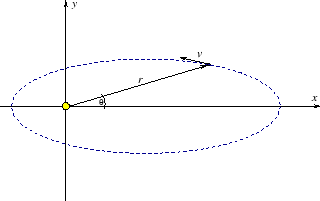
W celu udowodnienia praw Keplera rozważmy planetę o masie krążącą wokół gwiazdy o masie . Zakładamy, że masa gwiazdy jest znacznie większa od masy planety . Dzięki temu założeniu możemy przyjąć, że wpływ planety na ruch gwiazdy jest znikomy i gwiazda spoczywa. Położenie planety scharakteryzowane jest przez wektor . Na planetę działa tylko jedna siła - siła grawitacji pochodząca od gwiazdy, równa

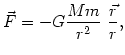(@1)

gdzie jest jednostkowym wektorem skierowanym od gwiazdy do planety, a znak minus oznacza, że siła jest przyciągająca. Druga zasada dynamiki Newtona ma w tym przypadku postać

(@2)

W problemie ruchu planety wokół gwiazdy zamiast używać współrzędnych kartezjańskich , wygodniej jest wprowadzić współrzędne biegunowe , charakteryzujące położenie ciała. Współrzędna oznacza odległość planety od gwiazdy, natomiast oznacza kąt, jaki tworzy wektor z osią . Związek współrzędnych kartezjańskich i biegunowych ma postać:

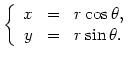(@3)

Wprowadzamy również wersory , związane ze współrzędnymi i . Wersor związany ze współrzędną jest wektorem jednostkowym skierowanym wzdłuż wektora . Wersor związany ze współrzędną jest wektorem jednostkowym prostopadłym do wersora i skierowanym w stronę większych kątów .

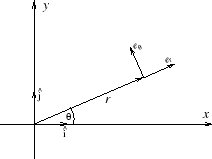
Kierunki wersorów , zmieniają się od punktu do punktu. Można je wyrazić przez wersory kartezjańskie i wzorami

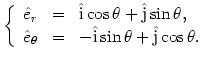(@4)

Gdy cząstka się porusza, wersory i się zmieniają. Pierwsze pochodne tych wersorów po czasie wynoszą

(@5)

gdzie jest prędkością kątową ciała. Różniczkując po czasie powyższe równania, dostajemy wyrażenia na drugie pochodne wersorów po czasie:

(@6)

Używając współrzędnych biegunowych, możemy zapisać, że położenie ciała wynosi

(@7)

Różniczkując to równanie po czasie i korzystając z wzorów na pochodną wersora po czasie, dostajemy, że prędkość we współrzędnych biegunowych wyraża się wzorem

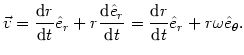(@8)

Różniczkując jeszcze raz i korzystając ze wzorów (@5,@6), otrzymujemy przyspieszenie wyrażone we współrzędnych biegunowych

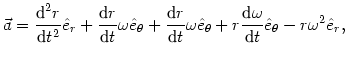(@9)

co daje ostatecznie

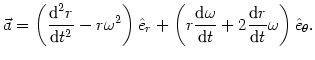(@10)

Pierwszy człon nosi nazwę przyspieszenia radialnego (jest to przyspieszenie w kierunku ), drugi człon nosi nazwę przyspieszenie transwersalnego (jest to przyspieszenie w kierunku ).

Podstawiając przyspieszenie zapisane we współrzędnych biegunowych do równania na dynamikę ruchu planety wokół gwiazdy (równanie @2), otrzymujemy

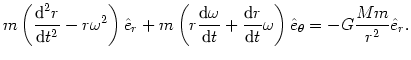(@11)

Powyższe równanie można zapisać jako dwa równania dla składowych:

(@12)

Drugie z tych równań można zapisać w formie:

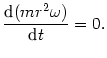(@13)

Oznacza to że wyrażenie, które jest różniczkowane, nie zmienia się w czasie:

(@14)

Wyrażenie powyższe jest równe momentowi pędu ciała

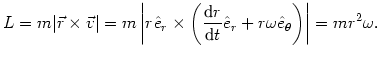(@15)

Moment pędu ciała jest więc stały. Stałość momentu pędu wynika wyłącznie z faktu, że siła grawitacji jest siłą centralną. Moment siły działający na planetę jest równy zeru, a co za tym idzie moment pędu ciała nie może ulec zmianie.

Pole, jakie zakreśla planeta w małym czasie , wynosi .

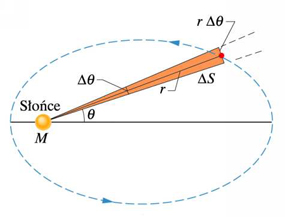
a) W przedziale czasu t linia łącząca planetę ze Słońcem o masie M (mająca w danej chwili długość r) zatacza kąt , zakreślając przy tym obszar (zacieniowany) o polu powierzchni S

Szybkość zmian pola wynosi więc

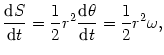(@16)

co oznacza, że prędkość polowa związana jest z momentem pędu wzorem

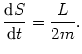(@17)

Ponieważ moment pędu jest stały, prędkość polowa jest również stała

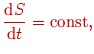(@18)

co tym samym dowodzi drugiego prawa Keplera.

Prędkość kątową ciała możemy wyrazić przez jego moment pędu

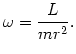(@19)

Podstawiając tę postać do pierwszego z równań (@12) otrzymujemy

(@20)

Chcemy udowodnić, że tor planety jest elipsą. W tym celu zastąpimy pochodną po czasie pochodną po

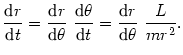(@21)

Różniczkując powyższe równanie po czasie, otrzymujemy

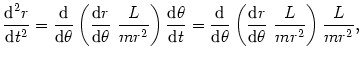(@22)

co można zapisać jako

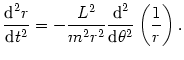(@23)

Podstawiając to do równania (@20), otrzymujemy

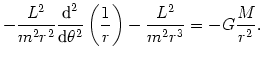(@24)

Po uproszczeniu powyższe równanie przyjmuje postać

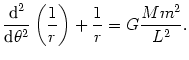(@25)

Jest to liniowe niejednorodne równanie różniczkowe na funkcję . Szczególne rozwiązanie równania niejednorodnego ma postać

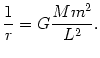(@26)

Ogólne rozwiązanie równania bez niejednorodności ma postać

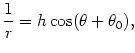(@27)

gdzie i są pewnymi stałymi. Ogólne rozwiązanie równanie z niejednorodnością ma w takim razie postać

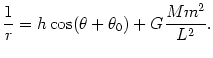(@28)

Wynika stąd, że tor planety opisany jest we współrzędnych biegunowych wzorem

(@29)

gdzie

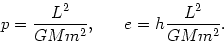(@30)

Dla powyższe równanie toru odpowiada hiperboli, dla paraboli, a dla elipsie. Stałą można wyrazić przez całkowitą energię układu (energię kinetyczną planety i energię potencjalną układu planeta-gwiazda) wzorem

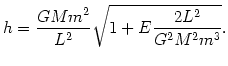(@31)

W związku z tym parametry i wyrażają się przez moment pędu planety i energię układu wzorami:

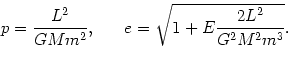(@32)

W zależności od energii układu, tor planety może być hiperbolą, parabolą lub elipsą. Jeśli

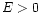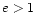• , to , co oznacza, że tor jest hiperbolą,
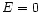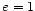• , to , co oznacza, że tor jest parabolą,
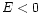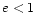• , to , co oznacza, że tor jest elipsą.

Jedyną możliwością odpowiadającą ograniczonemu ruchowi planety wokół gwiazdy jest elipsa, co tym samym dowodzi pierwszego prawa Keplera. Pozostałe możliwości (hiperbola, parabola) odpowiadają torom ciał, które mają wystarczająco dużą energię, aby uciec od gwiazdy do nieskończoności.

W przypadku, gdy tor jest elipsą, półosie elipsy (półoś wielka) i (półoś mała) można wyrazić przez parametry , wzorami

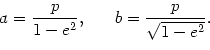(@33)

Pole elipsy o półosiach i wynosi

(@34)

Ponieważ prędkość polowa planety w jej ruchu wokół gwiazdy jest stała i równa

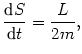(@35)

okres obiegu planety można obliczyć ze wzoru

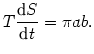(@36)

Podstawiając do powyższego wzoru wyrażenie na , po paru przekształceniach otrzymujemy, że okres obiegu planety wokół gwiazdy wynosi

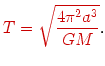(@37)

Zapisując to inaczej, mamy

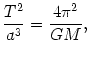(@38)

co tym samym dowodzi trzeciego prawa Keplera.