Modele Go

Niemal w każdej dyscyplinie naukowej istnieją zagadnienia, które mogą być bardzo skomplikowane, ale w wielu zastosowaniach wystarczy rozważać ich proste modele, jeśli ujmują one cechy najistotniejsze dla rozpatrywanego zastosowania. Na przykład w przypadku układów magnetycznych pierwszego wglądu w ich właściwości dostarcza model Isinga. Dla białek idea najprostszego sposobu modelowania została sformułowana w Japonii w 1976 i 1981 r. przez N. Go. Modele klasy Go opierają się na wielu doświadczalnych obserwacjach, świadczących o tym, że niemal o wszystkich właściwościach białek decyduje ich struktura natywna i to nawet wtedy, gdy białko jest w konformacjach rozwiniętych. Kontakty występujące w strukturze natywnej białka powinny więc pełnić wyróżnioną rolę w opisie teoretycznym białka. Zrealizować ten program można przez taki dobór potencjałów oddziaływań między aminokwasami, żeby w stanie natywnym realizowane było minimum energetyczne układu. W konformacjach wzbudzonych pojawiają się również kontakty nienatywne i należy je uznać za dużo słabsze, np. czysto odpychające, co zapobiega zapętlaniu się szkieletu polimeru ze sobą. Przykładem wyboru potencjału dla kontaktu natywnego jest potencjał Lennarda-Jonesa: 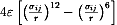, gdzie 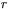oznacza odległość między parą aminokwasów (i, j), 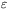charakterystyczną skalę energii, a parametr odległości 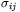dobiera się tak, by minimum potencjału odpowiadało odległości między atomami węgla C^α wyznaczonej doświadczalnie. Okazuje się, że tak uproszczony model daje bardzo podobne wyniki (Cieplak, T.X. Hoang, M.O. Robbins) do pełnoatomowej symulacji w badaniach mechanicznego rozciągania globularnego fragmentu ("domeny") tytyny — gigantycznego białka odpowiedzialnego za właściwości elastyczne mięśni (H. Lu, B. Isralewitz, A. Krammer, K. Vogel, K. Schulten). W badaniach rozciągania bada się np. wykres siły przeciwstawiającej się rozciąganiu w funkcji przemieszczenia końca białka.

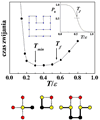
Rysunek 19. Definicja i właściwości modelu Go na dwuwymiarowej sieci

Rys. 19 przedstawia sieciową wersję modelu Go. Jest to model-zabawka. Składa się on z 16 połączonych ze sobą koralików poruszających się na sieci kwadratowej. Konformacja przedstawiona na rysunku jest tylko jedną z ponad 800 tys. możliwych i jedną z 37, które są maksymalnie zwarte — jest ułożona na sieci 4 x 4. Przyjmijmy, że wykreślona konformacja ma odpowiadać najniższej energii, a więc jest analogiem struktury białka wyznaczonej doświadczalnie. Niech koralik w prawym dolnym rogu odpowiada początkowi "białka". Dla tego układu istnieje 9 kontaktów natywnych: 1 - 14, 2 - 15, 3 - 16, 5 - 16, 6 - 9, 8 - 11, 9 - 16, 10 - 13, 10 - 15. Przypisujemy im energię 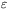. Pozostałe kontakty, np. 2 - 9, są nienatywne i im przypisujemy energię równą zero.

Ten układ jest na tyle krótki, że można ściśle numerycznie wyznaczyć sumę statystyczną i w szczególności wyznaczyć P₀ — równowagowe prawdopodobieństwo zdarzenia, że układ jest w stanie natywnym. P₀ jest z pewnością równe jedności dla T = 0 i zeru dla wysokich T. Temperatura, dla której P₀ osiąga wartość 0,5 oznaczana jest symbolem T_f. Jest to temperatura zwijania i jest ona miarą termodynamicznej stabilności układu. W realistycznych modelach oczekiwalibyśmy, że T_f powinno być rzędu 50 - 60 °C. Temperatura zwijania nic nie "mówi" na temat dynamiki układu. W klasycznych modelach pozasieciowych dynamikę wyznaczają równania Newtona, w których siły wynikają z potencjałów oddziaływania między aminokwasami. Można też uwzględniać wpływ rozpuszczalnika, który w szczególności określa temperaturę układu. Na sieci nie ma równań Newtona i możliwe są tylko ruchy dyskretne. Dynamikę trzeba tu zatem zdefiniować dodatkowo. Przypuśćmy, że dopuszczamy tylko takie ruchy, jakie są przedstawione w dolnym panelu rysunku: koralik oznaczony kolorem czarnym może przeskoczyć na miejsce zaznaczone kolorem czerwonym, jeśli nie jest ono zajęte. Jest to więc dynamika typu Monte Carlo. Dozwolony ruch jest na pewno realizowany, jeśli prowadzi do obniżenia energii Jeśli następowałoby podwyższenie energii, to ruch jest akceptowany z prawdopodobieństwem boltzmanowskim, a więc jest w ten sposób kontrolowany przez temperaturę.

Centralna część rysunku przedstawia wykres czasu zwijania w funkcji temperatury. Zdefiniowany jest on poprzez liczbę kroków Monte Carlo potrzebną do znalezienia się po raz pierwszy w stanie natywnym, jeśli konformacją początkową jest jakaś konformacja rozwinięta (wynik jest uśredniany po wielu takich konformacjach początkowych). Wykres ten ma kształt litery U. Czas zwijania jest długi dla dużych T, gdyż proces zwijania przypomina wtedy szukanie igły w stogu siana. Jest on również długi dla małych T, gdyż z powodu pojawienia się zjawisk szklistych układ trafia w lokalne minima energetyczne. Tak więc istnieje temperatura optymalna, T_min (ogólniej warunki optymalne, jeśli by także rozważyć zmiany pH), przy której zwijanie jest najszybsze. Ten wykres w kształcie U jest bardzo typowy — pojawia się on również i w modelach pozasieciowych i prawdziwych białkach. Duża szybkość zwijania dla T = T_min oznacza, że wtedy zwijanie jest najbardziej składne i odpowiada optymalnej średniej kolejności ruchów.

Dla rozpatrywanego tu modelu Go o 16 monomerach T_f jest większe niż T_min. Oznacza to, że dla T bliskiego T_f układ jest równowagowo blisko stanu natywnego, a efekty szkliste nie są jeszcze obecne. Jest to sytuacja analogiczna do tego, czego oczekuje się w białkach. Mówimy, że taki układ zwija się dobrze. Dla układów, które nie są modelami białek, ale przypadkowych sekwencji aminokwasów, T_f jest znacznie niższe niż T_min: przy schładzaniu układ "pułapkuje się" zanim znajdzie się blisko stanu natywnego. Takie układy zwijają się źle. Można pokazać (Cieplak, Hoang), że dla dostatecznie długich polimerów (na sieci i poza siecią) nawet modele Go przestają zwijać się dobrze. Istnieje więc granica funkcjonalności białka, która jest związana z jego rozmiarami.