Oddziaływania elektromagnetyczne

W tym rozdziale omówimy podstawowe procesy zachodzące pod wpływem oddziaływania elektromagnetycznego. Powstanie elektrodynamiki kwantowej - teorii opisującej takie procesy - jest nierozerwalnie związane ze sformułowaniem mechaniki kwantowej. Nie jest też zaskakujące to, iż oddziaływania elektromagnetyczne jako pierwsze doczekały się swojej teorii kwantowej. Zasadniczym punktem odniesienia była bowiem w tym przypadku maxwellowska elektrodynamika klasyczna oraz próby zastosowania jej do fizyki atomowej i opisu promieniowania atomów, badanych doświadczalnie już od połowy XIX wieku.

W trakcie rozwoju mechaniki kwantowej wiele wysiłku poświęcono badaniu układów kwantowych, np. elektronu, poruszających się w klasycznym zewnętrznym polu elektromagnetycznym. Nierelatywistyczne równanie Schrödingera opisujące w takiej sytuacji elektron o ładunku 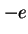ma postać

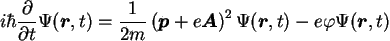[20]

gdzie 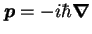jest operatorem pędu, 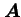jest potencjałem wektorowym, a 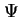jest nierelatywistyczną funkcją falową zależną od współrzędnych przestrzennych i czasu. Warto przypomnieć, że jeśli pole 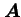opisuje stałe pole magnetyczne 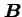(wtedy można wybrać 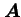w postaci 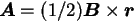), to z członu 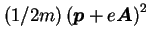otrzymuje się człon postaci 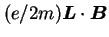, gdzie 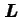jest operatorem orbitalnego momentu pędu. Człon ten interpretuje się jako oddziaływanie pola magnetycznego z momentem magnetycznym 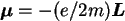elektronu poruszającego się w atomie. Zauważmy też, że współczynnik proporcjonalności w związku między momentem magnetycznym 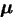i momentem pędu ma wartość klasyczną .

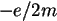Relatywistyczne efekty uwzględnia równanie Diraca

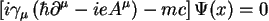[21]

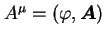w którym . Symbole 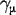, gdzie 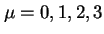, oznaczają tzw. macierze Diraca wymiaru 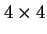działające na cztery składowe relatywistycznej funkcji falowej 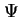, będącej tzw. spinorem Diraca, która opisuje elektron i pozyton, każdy o dwu możliwych rzutach spinu na wybraną oś kwantyzacji. Równanie to jest niezmiennicze względem przekształceń Lorentza (tzn. jest relatywistycznie niezmiennicze). Zauważmy też, że w równaniach (20) i (21) występują potencjały 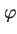oraz 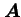, a nie pola 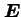i .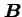

Jeśli w równaniu Diraca (21) za pole 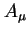przyjmiemy niezależne od czasu pole elektrostatyczne ciężkiego jądra atomowego, to równanie to daje nam teorię atomu wodoru (lub atomu wodoropodobnego, tj. atomu z jednym tylko elektronem). Interesujące jest zbadanie nierelatywistycznej granicy równania (21) w przypadku występowania statycznego pola magnetycznego 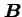. Odkrywamy wtedy spin elektronu: w granicy nierelatywistycznej równanie (21) sprowadza się bowiem do równania Pauliego

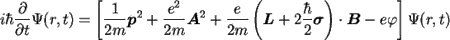[22]

w którym funkcja falowa 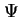ma dwie składowe, na które działają macierze Pauliego 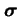; operator 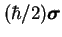jest właśnie operatorem spinu 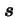elektronu. W nierelatywistycznym przybliżeniu równanie Diraca (21) opisuje więc także oddziaływanie spinu elektronu z polem magnetycznym 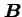. Są to wszystko rzeczy dobrze znane z mechaniki kwantowej i ich bardziej szczegółowa dyskusja nie jest przedmiotem tego artykułu. Zwróćmy tylko uwagę, że na podstawie klasycznych wyobrażeń (elektron jako kula o dobrze określonym promieniu, spin jako efekt obrotu jednorodnego rozkładu ładunku) moment magnetyczny elektronu, określający jego oddziaływanie z polem magnetycznym powinien wynosić 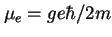z 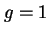. Z równania Diraca (21) wynika jednak, że dla elektronu 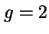, co znacznie lepiej zgadza się z doświadczeniem. Eksperymentalny pomiar czynnika 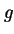i porównanie przewidywań teorii z tym pomiarem to w dużym stopniu historia rozwoju elektrodynamiki kwantowej.

Dotychczas dyskutowaliśmy opis w mechanice kwantowej elektronu poruszającego się w zewnętrznym polu elektromagnetycznym traktowanym klasycznie. Kwantowa teoria pola, jaką jest elektrodynamika kwantowa, to przede wszystkim teoria kwantowa pola elektromagnetycznego. U jej podstaw legły hipotezy Plancka i Einsteina oraz teoria Diraca. Istotną częścią elektrodynamiki kwantowej jest jeszcze jeden postulat, w pewnym sensie odwrotny do kwantowania pola elektromagnetycznego. Szukając jednolitej teorii elektronów oddziałujących z polem elektromagnetycznym, postulujemy mianowicie, że elektronowi, który klasycznie jest cząstką, odpowiada także pewne pole fizyczne 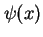(należy tu podkreślić, że pole 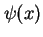ma inny sens fizyczny niż funkcja falowa 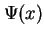elektronu w mechanice kwantowej), którego kwantami są właśnie elektrony i pozytony. W efekcie otrzymujemy w pełni kwantową teorię pól elektronowego 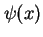i elektromagnetycznego 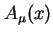, których kwantami są odpowiednio elektrony i pozytony oraz fotony.