Znaczenie renormalizowalności. Model Standardowy jako teoria efektywna
Można zadać pytanie, dlaczego trzeba było kilkudziesięciu lat, żeby w pełni zrozumieć naturę oddziaływań słabych i silnych. Przecież procesy takie jak rozpad β czy α charakteryzują się skalą energii rzędu MeV, od dawna osiągalną w warunkach laboratoryjnych. Można by więc sądzić, iż procesy te mogły być szczegółowo przebadane i zrozumiane już dawno. Okazuje się jednak, że kluczem do zrozumienia tych zjawisk, zachodzących nawet spontanicznie (promieniotwórczość naturalna), są procesy zachodzące przy znacznie wyższych energiach. Inaczej mówiąc, do zrozumienia struktury materii na odległościach rzędu 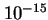 m trzeba było ją zrozumieć na odległościach rzędu
m trzeba było ją zrozumieć na odległościach rzędu 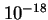 m. To zaś wymaga olbrzymich energii zderzanych cząstek, jakie udaje się osiągnąć w akceleratorach dopiero od niedawna. Takie powiązanie "świata cząstek lekkich" ze "światem cząstek ciężkich", zaskakujące na poziomie fizyki klasycznej, ma swoje głębokie źródło w kwantowej naturze budowy materii. W układach podlegających prawom kwantowym obowiązuje zasada nieoznaczoności wiążąca energię i czas. Najbardziej znanym jej przejawem jest związek czasu życia stanu rezonansowego z jego szerokością tzn. z nieoznaczonością jego energii. W kwantowej teorii pola przejawem zasady nieoznaczoności jest fakt, że wymiana bardzo ciężkich cząstek wirtualnych z reguły wpływa na oddziaływania cząstek lekkich, zachodzące przy energiach
m. To zaś wymaga olbrzymich energii zderzanych cząstek, jakie udaje się osiągnąć w akceleratorach dopiero od niedawna. Takie powiązanie "świata cząstek lekkich" ze "światem cząstek ciężkich", zaskakujące na poziomie fizyki klasycznej, ma swoje głębokie źródło w kwantowej naturze budowy materii. W układach podlegających prawom kwantowym obowiązuje zasada nieoznaczoności wiążąca energię i czas. Najbardziej znanym jej przejawem jest związek czasu życia stanu rezonansowego z jego szerokością tzn. z nieoznaczonością jego energii. W kwantowej teorii pola przejawem zasady nieoznaczoności jest fakt, że wymiana bardzo ciężkich cząstek wirtualnych z reguły wpływa na oddziaływania cząstek lekkich, zachodzące przy energiach 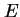 dużo mniejszych od skali mas
dużo mniejszych od skali mas 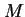 cząstek wirtualnych. Tym samym fizyka na bardzo małych odległościach wpływa na zjawiska zachodzące na odległościach dużo większych. W tej sytuacji narzuca się natychmiast pytanie odwrotne: skoro stwierdziliśmy, że zjawiska zachodzące przy bardzo różnych skalach energii (na bardzo różnych odległościach) są wzajemnie ze sobą powiązane, to co jest odpowiedzialne za fakt, że jednak udaje nam się co jakiś czas zrozumieć strukturę materii w pewnych etapach znaczonych skalami energii dostępnych w kolejnych generacjach doświadczeń? Jest to dobry moment by poświęcić nieco miejsca renormalizowalnym i efektywnym teoriom pola. Opis współzależności fizyki przy różnych skalach energii upraszcza się w istotny sposób, gdy zjawiska zachodzące w pewnym obszarze energii
cząstek wirtualnych. Tym samym fizyka na bardzo małych odległościach wpływa na zjawiska zachodzące na odległościach dużo większych. W tej sytuacji narzuca się natychmiast pytanie odwrotne: skoro stwierdziliśmy, że zjawiska zachodzące przy bardzo różnych skalach energii (na bardzo różnych odległościach) są wzajemnie ze sobą powiązane, to co jest odpowiedzialne za fakt, że jednak udaje nam się co jakiś czas zrozumieć strukturę materii w pewnych etapach znaczonych skalami energii dostępnych w kolejnych generacjach doświadczeń? Jest to dobry moment by poświęcić nieco miejsca renormalizowalnym i efektywnym teoriom pola. Opis współzależności fizyki przy różnych skalach energii upraszcza się w istotny sposób, gdy zjawiska zachodzące w pewnym obszarze energii 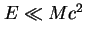 (gdzie
(gdzie 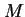 jest skalą mas być może istniejących i nieodkrytych jeszcze cząstek niedostępnych kinematycznie w doświadczeniu) daje się zrozumieć w języku renormalizowalnej kwantowej teorii pola. Podstawową cechą renormalizowalnych teorii efektywnych jest to, iż dominujące efekty (czyli takie, które nie maleją, gdy M rośnie) nieznanej fizyki (tj. efekty wymian wirtualnych ciężkich cząstek o masach
jest skalą mas być może istniejących i nieodkrytych jeszcze cząstek niedostępnych kinematycznie w doświadczeniu) daje się zrozumieć w języku renormalizowalnej kwantowej teorii pola. Podstawową cechą renormalizowalnych teorii efektywnych jest to, iż dominujące efekty (czyli takie, które nie maleją, gdy M rośnie) nieznanej fizyki (tj. efekty wymian wirtualnych ciężkich cząstek o masach 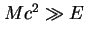 , których taka teoria nie opisuje) można ukryć w skończonej liczbie swobodnych parametrów takiej teorii, wyznaczanych przez porównanie skończonej liczby jej przewidywań z danymi doświadczalnymi otrzymywanymi przy niskich energiach. Pozostałe przewidywania takiej teorii można wówczas podawać z dowolną w zasadzie dokładnością w funkcji tych parametrów. Nie znaczy to oczywiście, że teoria taka jest ścisła. Nieuwzględniana przez tę teorię fizyka przy skali
, których taka teoria nie opisuje) można ukryć w skończonej liczbie swobodnych parametrów takiej teorii, wyznaczanych przez porównanie skończonej liczby jej przewidywań z danymi doświadczalnymi otrzymywanymi przy niskich energiach. Pozostałe przewidywania takiej teorii można wówczas podawać z dowolną w zasadzie dokładnością w funkcji tych parametrów. Nie znaczy to oczywiście, że teoria taka jest ścisła. Nieuwzględniana przez tę teorię fizyka przy skali 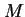 może przejawiać się w odstępstwie rzędu
może przejawiać się w odstępstwie rzędu 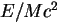 przewidywań teorii renormalizowalnej od wyników pomiarów eksperymentalnych. Takie zależne od
przewidywań teorii renormalizowalnej od wyników pomiarów eksperymentalnych. Takie zależne od 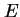 i
i 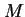 efekty można odkryć dopiero przy odpowiedniej precyzji doświadczalnej z jednej strony i obliczeń teoretycznych wykonywanych w teorii renormalizowalnej z drugiej strony. Zaletą teorii renormalizowalnej jest więc to, że potrafi ona z bardzo dobrym przybliżeniem opisać zjawiska zachodzące w pewnym zakresie energii. Z drugiej strony, sformułowanie teorii renormalizowalnej poprawnie opisującej jakiś zakres energii jest pewnym etapem w penetrowaniu struktury materii, który trudno przekroczyć, gdyż wymaga to albo osiągnięcia doświadczalnie energii
efekty można odkryć dopiero przy odpowiedniej precyzji doświadczalnej z jednej strony i obliczeń teoretycznych wykonywanych w teorii renormalizowalnej z drugiej strony. Zaletą teorii renormalizowalnej jest więc to, że potrafi ona z bardzo dobrym przybliżeniem opisać zjawiska zachodzące w pewnym zakresie energii. Z drugiej strony, sformułowanie teorii renormalizowalnej poprawnie opisującej jakiś zakres energii jest pewnym etapem w penetrowaniu struktury materii, który trudno przekroczyć, gdyż wymaga to albo osiągnięcia doświadczalnie energii 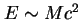 , albo dokładności pomiarów rzędu
, albo dokładności pomiarów rzędu 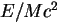 . Interesującym przykładem jest tu elektrodynamika kwantowa, będąca teorią renormalizowalną i zarazem przybliżeniem niskoenergetycznym pełnej teorii elektrosłabej. Bliższe spojrzenie na wzajemną relację tych dwóch teorii ułatwi nam dyskusję współczesnych kierunków badań. Jednym z najbardziej spektakularnych sukcesów elektrodynamiki kwantowej jest zgodność mierzonego momentu magnetycznego mionu z przewidywaniem tej teorii. Jeśli jednak spojrzymy na elektrodynamikę kwantową jak na teorię efektywną, to nowa fizyka (którą z punktu widzenia elektrodynamiki są oddziaływania słabe, czyli przenoszące je bozony
. Interesującym przykładem jest tu elektrodynamika kwantowa, będąca teorią renormalizowalną i zarazem przybliżeniem niskoenergetycznym pełnej teorii elektrosłabej. Bliższe spojrzenie na wzajemną relację tych dwóch teorii ułatwi nam dyskusję współczesnych kierunków badań. Jednym z najbardziej spektakularnych sukcesów elektrodynamiki kwantowej jest zgodność mierzonego momentu magnetycznego mionu z przewidywaniem tej teorii. Jeśli jednak spojrzymy na elektrodynamikę kwantową jak na teorię efektywną, to nowa fizyka (którą z punktu widzenia elektrodynamiki są oddziaływania słabe, czyli przenoszące je bozony 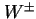 i
i 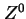 ) może dawać dodatkowy przyczynek do obliczanego teoretycznie momentu magnetycznego mionu. Dopiero w doświadczeniu przeprowadzanym aktualnie (tj. w roku 2003) w amerykańskim Narodowym Laboratorium w Brookhaven moment ten zmierzony ma być z dokładnością pozwalającą na wykrycie takiego dodatkowego wkładu, którego sama elektrodynamika nie opisuje. Tak więc doświadczenie to odkryłoby istnienie nowej fizyki przy skali
) może dawać dodatkowy przyczynek do obliczanego teoretycznie momentu magnetycznego mionu. Dopiero w doświadczeniu przeprowadzanym aktualnie (tj. w roku 2003) w amerykańskim Narodowym Laboratorium w Brookhaven moment ten zmierzony ma być z dokładnością pozwalającą na wykrycie takiego dodatkowego wkładu, którego sama elektrodynamika nie opisuje. Tak więc doświadczenie to odkryłoby istnienie nowej fizyki przy skali 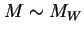 nawet wtedy, gdybyśmy nie znali jeszcze teorii standardowej i nie osiągnęli w akceleratorach energii
nawet wtedy, gdybyśmy nie znali jeszcze teorii standardowej i nie osiągnęli w akceleratorach energii 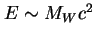 . Oczywiście teoria elektrosłaba powstała znacznie wcześniej niż możliwe stały się odpowiednio dokładne pomiary momentu magnetycznego mionu. Było to możliwe dzięki temu, że wymiany ciężkich cząstek obecnych w teorii elektrosłabej, dające poprawki do przewidywań elektrodynamiki kwantowej, przejawiają się w przyrodzie także przez pozornie odmienny typ oddziaływań (nie zachowują one pewnych liczb kwantowych, zachowywanych przez oddziaływania elektromagnetyczne) i zostały odkryte jako oddziaływania słabe, których efektywnym niskoenergetycznym opisem jest nierenormalizowalna teoria Fermiego. Żądanie renormalizowalności tej ostatniej doprowadziło właśnie do powstania Teorii Standardowej. Jej znajomość oraz znajomość wyznaczonych doświadczalnie jej parametrów (mas bozonów cechowania, wartości stałych sprzężenia) umożliwia obecnie ścisłe obliczenie tej części wkładu nowej fizyki do momentu magnetycznego mionu, która jest spowodowana wymianami bozonów
. Oczywiście teoria elektrosłaba powstała znacznie wcześniej niż możliwe stały się odpowiednio dokładne pomiary momentu magnetycznego mionu. Było to możliwe dzięki temu, że wymiany ciężkich cząstek obecnych w teorii elektrosłabej, dające poprawki do przewidywań elektrodynamiki kwantowej, przejawiają się w przyrodzie także przez pozornie odmienny typ oddziaływań (nie zachowują one pewnych liczb kwantowych, zachowywanych przez oddziaływania elektromagnetyczne) i zostały odkryte jako oddziaływania słabe, których efektywnym niskoenergetycznym opisem jest nierenormalizowalna teoria Fermiego. Żądanie renormalizowalności tej ostatniej doprowadziło właśnie do powstania Teorii Standardowej. Jej znajomość oraz znajomość wyznaczonych doświadczalnie jej parametrów (mas bozonów cechowania, wartości stałych sprzężenia) umożliwia obecnie ścisłe obliczenie tej części wkładu nowej fizyki do momentu magnetycznego mionu, która jest spowodowana wymianami bozonów 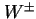 i
i 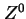 . Jeśli wkłady te nie wystarczą do wyjaśnienia odstępstwa momentu magnetycznego obliczonego w ramach elektrodynamiki od jego mierzonej wartości, będziemy raczej skłonni przypisać to nie załamaniu się podstaw Teorii Standardowej, ale istnieniu jeszcze innych nowych cząstek o masach rzędu 100 GeV.
. Jeśli wkłady te nie wystarczą do wyjaśnienia odstępstwa momentu magnetycznego obliczonego w ramach elektrodynamiki od jego mierzonej wartości, będziemy raczej skłonni przypisać to nie załamaniu się podstaw Teorii Standardowej, ale istnieniu jeszcze innych nowych cząstek o masach rzędu 100 GeV.
Podobnie należy też prawdopodobnie interpretować bardzo niewielkie lecz niezerowe masy neutrin. W Teorii Standardowej można je łatwo uwzględnić nie psując renormalizowalności. W poprzednim rozdziale podaliśmy jednak argumenty za tym, że mała ich wartość powstaje naturalnie, jeśli w próżni istnieje oddziałujące z prawoskrętnymi neutrinami i lewoskrętnymi antyneutrinami stałe pole 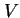 o wartości wiele rzędów wielkości większej niż skala kondensatu pola Higgsa
o wartości wiele rzędów wielkości większej niż skala kondensatu pola Higgsa 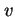 naruszającego symetrię
naruszającego symetrię 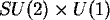 . Występowanie takiego stałego pola
. Występowanie takiego stałego pola 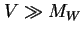 najprościej interpretować jako nieznikającą wartość próżniową jakiegoś pola skalarnego
najprościej interpretować jako nieznikającą wartość próżniową jakiegoś pola skalarnego 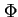 , którego kwantami są cząstki o masach
, którego kwantami są cząstki o masach 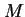 rzędu
rzędu 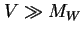 , i które nie są uwzględnione w Teorii Standardowej będącej teorią efektywną w stosunku do teorii, w której pole
, i które nie są uwzględnione w Teorii Standardowej będącej teorią efektywną w stosunku do teorii, w której pole 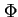 występuje. Przy takim podejściu obserwowane przy niskich energiach masy neutrin stają się efektami rzędu
występuje. Przy takim podejściu obserwowane przy niskich energiach masy neutrin stają się efektami rzędu 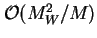 , których nie opisuje renormalizowalna Teoria Standardowa. Można je jednak opisywać, uwzględniając nierenormalizowalne oddziaływanie, tak jak efekty oddziaływań słabych uwzględnia się w elektrodynamice poprzez nierenormalizowalne oddziaływanie Fermiego.
, których nie opisuje renormalizowalna Teoria Standardowa. Można je jednak opisywać, uwzględniając nierenormalizowalne oddziaływanie, tak jak efekty oddziaływań słabych uwzględnia się w elektrodynamice poprzez nierenormalizowalne oddziaływanie Fermiego.





