Algorytm gradientów sprzężonych

W celu przezwyciężenia wad algorytmu backpropagation, takich jak:

• powolność algorytmu
• tendencja do zatrzymywania się algorytmu w minimach lokalnych funkcji

stosuje się czasem także inne metody uczenia. Jedną z bardziej znanych alternatywnych metod uczenia jest algorytm gradientów sprzężonych. Jest on zwykle znacznie szybszy od algorytmu wstecznej propagacji błędów. Ponadto zaletą tego algorytmu jest fakt, że nie ma on parametrów takich jak współczynnik uczenia oraz momentum, których wartości powinny być zaproponowane przez użytkownika. Dzięki wymienionym zaletom algorytm gradientów sprzężonych jest prostszy i wygodniejszy w użyciu niż backpropagation (stwierdzenie to wymaga dodatkowego wyjaśnienia: realizacja pojedynczej epoki uczenia w metodzie gradientów sprzężonych wymaga zauważalnie dłuższego czasu niż realizacja pojedynczej epoki w metodzie wstecznej propagacji błędów, co może wydawać się niekorzystne; ponieważ jednak liczba realizowanych powtórzeń epoki uczenia w tym algorytmie zwykle jest znacznie mniejsza niż w backpropagation, algorytm ten jest korzystniejszy). Przedstawimy regułę, zgodnie z którą działa algorytm. Najpierw obierany jest pewien "sensowny kierunek" ruchu po wielowymiarowej powierzchni błędu. Następnie w kierunku tym prowadzona jest po powierzchni błędów linia prosta i wyznaczane jest minimum funkcji błędów dla wszystkich punktów leżących wzdłuż tej prostej. Korzystamy tu z faktu, że wyznaczenie minimum funkcji wzdłuż zadanej prostej jest zadaniem relatywnie prostym, do rozwiązania którego stosowane są bardzo szybkie algorytmy, np. pewne formy algorytmu bisekcji. Po znalezieniu minimum wzdłuż zadanego początkowo kierunku, z miejsca położenia tego minimum wyznacza się nowy "sensowny kierunek" i cały ten proces jest powtarzany. Nie ulega wątpliwości, że postępując w opisany wyżej sposób będziemy stale posuwali się w kierunku malejących wartości funkcji błędu i osiągniemy wreszcie punkt, który będzie minimum tej funkcji. Niestety może się zdarzyć, że opisany proces poszukiwań zakończy się w jednym z minimów lokalnych nie docierając do minimum globalnego, ale na to nie ma rady.

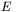
Wybór kierunku ruchu po wielowymiarowej powierzchni błędu Przytoczony wyżej opis metody wydaje się jasny i raczej zrozumiały. Wątpliwości może budzić jedynie zastosowane w tym kontekście wyrażenie "sensowny kierunek". Jaki to jest ten sensowny kierunek? Na pozór oczywistym wyborem byłoby zastosowanie kierunku największego spadku (a więc tego samego kierunku, który stosowany jest w metodzie wstecznej propagacji błędów). W rzeczywistości ten intuicyjnie oczywisty kierunek okazuje się raczej zły. Przeprowadzając minimalizację wzdłuż jednego wybranego kierunku narażamy się na to, że następna linia wyznaczona zgodnie z regułą największego spadku może "zniszczyć" rezultaty minimalizacji wzdłuż początkowego kierunku. Okazuje się, że w przypadku stosowania wyłącznie zasady największego spadku przy wyznaczaniu kolejnych kierunków poszukiwań, nawet na takiej prostej powierzchni jak paraboloida będzie potrzebne przeprowadzenie dużej liczby poszukiwań wzdłuż kolejno proponowanych prostych. W tej sytuacji lepszym rozwiązaniem jest tu wybór tzw. kierunków sprzężonych, czyli "nie wpływających na siebie". Stąd pochodzi zresztą nazwa opisywanej tu metody.

Przy tworzeniu tego algorytmu zastosowano następujący pomysł: po przeprowadzeniu już minimalizacji funkcji błędów w pewnym wybranym kierunku trzeba potem zadbać o to, by tego wyniku nie zaprzepaścić w kolejnych etapach optymalizacji. Można to osiągnąć, jeśli druga pochodna wyznaczona w tym kierunku zostanie przy dalszych krokach uczenia utrzymana na poziomie zerowym. Aby utrzymać zerową wartość drugiej pochodnej wyznacza się właśnie kierunki sprzężone do kierunku wcześniej wykorzystywanego, gdyż łatwo jest wykazać, że posuwanie się w kierunku sprzężonym nie powoduje zmiany ustalonej (zerowej) wartości drugiej pochodnej, obliczanej wzdłuż poprzednio wybranego kierunku. Przy wyznaczaniu kierunku sprzężonego wykorzystuje się założenie, mówiące, że powierzchnia błędu ma kształt paraboliczny. Oczywiście w rzeczywistości założenie to prawie zawsze nie odpowiada rzeczywistemu kształtowi powierzchni błędu, ponieważ przeprowadzone przez różnych autorów symulacje i projekcje wykazują, że powierzchnia ta jest poryta przez liczne rozpadliny i wąwozy. Upraszczając sytuację można zakładać, że przynajmniej lokalnie mamy tu do czynienia z gładką powierzchnią. Jeśli to założenie jest spełnione (przynajmniej w przybliżeniu), to wystarcza 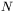epok procesu uczenia (gdzie 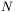jest wymiarem przestrzeni sygnałów wejściowych), aby osiągnąć minimum. W rzeczywistości na złożonej powierzchni błędu dokładne sprzężenie kierunków zawodzi, w związku z czym liczba kroków uczenia jest z reguły większa od 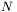, ale i tak w typowych przypadkach metoda gradientów sprzężonych wymaga realizacji znacznie mniejszej liczby epok niż metoda wstecznej propagacji błędów, ponadto jest ona zbieżna do lepszego (dokładniej osiąganego) minimum. Jest to konsekwencja faktu, że algorytm poszukiwania najmniejszej wartości funkcji wzdłuż zadanego kierunku usadawia się dokładnie w punkcie minimum kierunkowego, które jest też minimum całej wielowymiarowej funkcji błędu, jeśli wybrany na pewnym etapie kierunek przez takie minimum przechodzi. Algorytm wstecznej propagacji błędów może wielokrotnie przeskakiwać przez punkt minimum — żeby to minimum dokładnie osiągnąć musiałby zostać uruchomiony z bardzo niewielkim współczynnikiem uczenia (rys. 7).

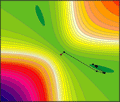
Rysunek 7. Przebieg procesu uczenia sterowany algorytmem gradientów sprzężonych; minimum funkcji błędu osiagnięto po 22 iteracjach

wyraźnie wskazuje na wyższość algorytmu gradientów sprzężonych nad zwykłą wsteczną propagacją, która jednak jest z pewnością metodą uczenia bardziej uniwersalną.