Uczenie sieci jako proces minimalizacji błędu
Skoro wprowadziliśmy już pojęcie powierzchni błędu, to możemy (co jest wygodne) stwierdzić, że celem uczenia sieci jest znalezienie na wielowymiarowej powierzchni błędu punktu o najmniejszej wysokości. Innymi słowy w procesie uczenia chodzi o ustalenie takiego zestawu wag i progów, który odpowiada najmniejszej wartości błędu. W niektórych przypadkach jest to łatwe, np. jak już było wspomniane, przy stosowaniu modeli liniowych z funkcją błędu opartą na sumie kwadratów, powierzchnia błędu ma kształt paraboloidy (wielowymiarowej funkcji kwadratowej). Taki kształt funkcji błędu jest bardzo korzystny, ponieważ ma formę kielicha o gładkich powierzchniach bocznych i z jednym wyraźnym minimum. W tym przypadku wyznaczenie wartości minimalnej nie stwarza większych problemów (patrz rys. 4), co zresztą ma niewielkie znaczenie praktyczne, gdyż dla modeli liniowych zestaw optymalnych parametrów najczęściej może być wyznaczony obliczeniowo, bez konieczności uczenia sieci. Niestety, dla sieci neuronowej budującej model nieliniowy proces nie jest już ani tak łatwy, ani tak skuteczny. Oczywiście każde zadanie, jakie zamierzamy rozwiązać przy użyciu sieci neuropodobnych, ma swoje odrębne, unikatowe właściwości, przejawiające się głównie w postaci rozmaitych "zafalowań" powierzchni błędów. Na setkach przykładów wykazano jednak, że typowa powierzchnia błędu dla typowego zadania rozwiązywanego przez sieć nieliniową jest o wiele bardziej złożona niż opisany wyżej model gładkiej paraboloidy.problemy związane z powierzchnią błędu Powierzchnia taka ma pewne cechy, mogące być źródłem wielu problemów: występują na niej minima lokalne (punkty położone niżej, niż otaczający "teren", ale powyżej minimum globalnego), do których proces uczenie łatwo "wpada", a z których ucząca się sieć nie może się potem "wyzwolić" (rys. 5).
Rysunek 5. Przykładowa powierzchnia błędu przy uczeniu sieci nieliniowej zawierająca, obok minimum wlaściwego, dodatkowe (płytsze) minimum lokalne
(aby obejrzeć powiększony rysunek, kliknij w miniaturkę)
Na takiej powierzchni błędu występują też często rozległe płaskie powierzchnie — obszary plateau, na których algorytmy uczenia, napędzane i sterowane w istocie wielkością i kierunkiem nachylenia powierzchni (czyli gradientem malejącego błędu) znacznie zwalniają swoją pracę. Pułapką są też punkty siodłowe, w których proces uczenia lubi utknąć (gradient funkcji błędu na "siodle" jest zerowy) a także, najbardziej nieprzyjemne, długie, wąskie wąwozy, w których procesy uczenia "obijają się o ściany" nie osiągając przez długi czas znaczącego postępu w aktywnym zmniejszaniu błędu, pomimo setek pokazów elementów zbioru uczącego. Jeśli proces uczenia nieliniowych sieci związany jest z wieloma niedoskonałościami, to określenie minimum globalnego powierzchni błędu dla tych sieci w sposób analityczny w ogóle nie jest możliwe. Dlatego uczenie nieliniowej sieci neuronowej można uznać za jedyną w zasadzie możliwość w zakresie eksploracyjnego badania powierzchni błędu odpowiadającej posiadanemu zbiorowi danych uczących. Jest wiele metod takiego uczenia i omówimy najpopularniejsze. Opis działania rozważanych algorytmów uczenia sieci przedstawiony zostanie w oparciu o ciąg uczący o postaci:
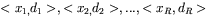 |
[8] |
gdzie wartości wejściowe 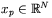 (
(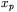 — sygnał wejściowy pokazywany sieci podczas kroku uczenia o numerze
— sygnał wejściowy pokazywany sieci podczas kroku uczenia o numerze 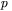 ;
; 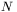 — liczba składowych wektora sygnałów wejściowych,
— liczba składowych wektora sygnałów wejściowych, 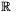 — zbiór liczb rzeczywistych), zaś oczekiwane (zakładane) wartości wyjściowe
— zbiór liczb rzeczywistych), zaś oczekiwane (zakładane) wartości wyjściowe 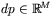 są określone dla każdego
są określone dla każdego 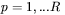 , gdzie
, gdzie 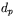 oznacza wzorcowy sygnał wyjściowy oczekiwany na wyjściu sieci podczas realizacji kroku uczenia o numerze
oznacza wzorcowy sygnał wyjściowy oczekiwany na wyjściu sieci podczas realizacji kroku uczenia o numerze 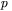 ,
, 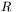 — liczbę dostępnych danych w zbiorze uczącym, natomiat
— liczbę dostępnych danych w zbiorze uczącym, natomiat 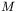 — liczbę sygnałów wyjściowych z całej sieci. Podczas działania sieci neuronowej (przyjmiemy architekturę sieci jednokierunkowej z jedną warstwą ukrytą zawierającą
— liczbę sygnałów wyjściowych z całej sieci. Podczas działania sieci neuronowej (przyjmiemy architekturę sieci jednokierunkowej z jedną warstwą ukrytą zawierającą 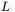 neuronów) wyróżnić można następujące etapy:
neuronów) wyróżnić można następujące etapy:
- wprowadzenie na wejście sieci
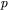 -tego wektora wejściowego (
-tego wektora wejściowego (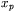 ),
), - obliczenie dla każdego neuronu warstwy ukrytej wartości zbiorczego (sumarycznego) sygnału
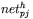 pobudzenia neuronu o numerze
pobudzenia neuronu o numerze 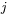 należącego do warstwy ukrytej, powstającego w wyniku prezentacji elementu zbioru uczącego o numerze
należącego do warstwy ukrytej, powstającego w wyniku prezentacji elementu zbioru uczącego o numerze 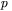 zgodnie ze wzorem:
zgodnie ze wzorem:
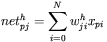
[9] - obliczenie wartości wyjściowej
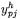 dla każdego neuronu warstwy ukrytej:
dla każdego neuronu warstwy ukrytej:
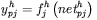
[10] - obliczenie dla każdego neuronu warstwy wyjściowej wartości zbiorczego (sumarycznego) sygnału
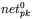 pobudzenia neuronu o numerze
pobudzenia neuronu o numerze 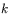 należącego do warstwy wyjściowej, powstającego w wyniku prezentacji elementu zbioru uczącego o numerze
należącego do warstwy wyjściowej, powstającego w wyniku prezentacji elementu zbioru uczącego o numerze 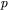 (przy czym
(przy czym 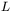 jest liczbą sygnałów wyjściowych z danej warstwy, a
jest liczbą sygnałów wyjściowych z danej warstwy, a 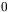 pisane jako indeks górny oznacza sygnały odnoszące się do neuronów warstwy wyjściowej):
pisane jako indeks górny oznacza sygnały odnoszące się do neuronów warstwy wyjściowej):
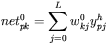
[11] - obliczenie wartości wyjściowej dla każdego neuronu warstwy wyjściowej:
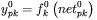
[12]
W prawidłowo działającej sieci wektor wartości wyjściowych 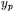 powinien być identyczny lub bardzo zbliżony do wektora wartości oczekiwanych
powinien być identyczny lub bardzo zbliżony do wektora wartości oczekiwanych 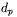 . Aby do tego doprowadzić stosuje się różne algorytmy uczenia, które zostaną przedstawione.
. Aby do tego doprowadzić stosuje się różne algorytmy uczenia, które zostaną przedstawione.





